7.2. Filtragem de Dados Oriundos de Séries Temporais de Imagens de Satélite
Uma série temporal gerada por imagens de satélite pode estar sujeita à ocorrência de ruídos oriundos de diversos fatores como a presença de nuvens, falhas do detector, geometria de iluminação e visada, dentre outros [121, 123, 135]. Para minimizar os efeitos dos ruídos em séries temporais foram criados diversos filtros. Neste sentido, Hird and McDermid [135] testaram seis filtros e concluíram que quatro deles produziram bons resultados:
Além deles, também podem ser utilizados os filtros Hants que têm por base a transformada de Fourier [119].
7.2.1. 4253H twice
Este filtro é uma adequação do filtro de mediana proposto por Velleman [136]. A parte numérica do nome do filtro 4253 representa a largura da janela temporal utilizada para o cálculo da mediana. Por exemplo, inicialmente o filtro considera uma janela de quatro datas. A partir das quatro primeiras datas é calculado um valor da primeira mediana. Na sequência a janela é deslocada uma data no tempo e, é composta pelos dados das três últimas datas da janela anterior mais a data seguinte e assim sucessivamente até a última data da série temporal do período considerado. Na segunda, terceira e quarta rodadas do filtro as janelas têm tamanho de 2, 5 e 3 datas, respectivamente. O termo H do nome do filtro refere-se à função de Hann e o twice é devido à função ser aplicada tanto nos dados quanto nos resíduos. A função de Hann ou Hanning representa uma função simétrica utilizada para filtrar os dados, cujo maior peso é dado ao elemento central da janela. Para calcular os coeficientes da função de Hann, deve-se resolver a Equação 7.1:
em que \(N\) representa o número total de elementos da janela, \(n\) o elemento que será calculado, e \(w\) o valor do coeficiente calculado para o elemento \(n\).
Inicialmente, o filtro de medianas, com as janelas (\(v\)) de tamanho 4, 2, 5 e 3, é aplicado à série temporal (\(x_t\)) no tempo \(t\). Para o caso de \(n\) ser um número ímpar a Equação 7.2 deve ser utilizada:
em que \(v = 2u+1\) e \(y_t\) referem-se ao valor de mediana para o elemento na posição \(t\).
Quando \(v\) for um número par, a Equação 7.3 deve ser utilizada:
em que \(v = 2u\) e \(y_{t+\frac{1}{2}}\) referem-se ao valor médio determinado a partir das duas posições centrais da janela.
Na série filtrada resultante é aplicada a função de Hann com uma janela de tamanho 3 (Equação 7.4):
em que \(z_t\) refere-se ao valor do elemento e \(y_t\) é o valor mediano no tempo \(t\).
Após esta nova filtragem é calculado o resíduo entre os dados originais e os dados filtrados (Equação 7.5):
em que \(r_t\) refere-se ao valor do resíduo do elemento no tempo \(t\).
A mesma seqüência de filtros é aplicada aos resíduos (\(r_t\)) e o resultado da filtragem dos resíduos é somado aos dados filtrados [136].
7.2.2. Savitzky–Golay
O filtro de Savitzky–Golay [137] é um clássico entre os filtros de suavização de sinais analíticos, de séries temporais ou de sinais. A equação para o filtro Savitzky-Golay é baseada em um ajuste polinomial de uma janela deslizante de dados. Para aplicar este filtro, os seguintes passos devem ser realizados:
definir a largura da janela temporal
remover o ponto central do intervalo abrangido pela janela
ajustar, pelo método dos mínimos quadrados, um polinômio de grau variável aos dados restantes
utilizar o polinômio para estimar o valor do ponto removido e substituir este valor
deslocar a janela para o próximo ponto e repetir o processo anterior.
A equação geral deste filtro é apresentada na Equação 7.6:
em que: \(y_t\) refere-se ao valor filtrado no tempo \(t\); \(x_{t+i}\) são os valores dos dados nas posições em torno de \(t\), com \(i\) variando entre \(-u\) e \(u\); \(v\) é uma constante de normalização (Equação 7.7) que é a soma dos coeficientes, garantindo que a média dos coeficientes seja igua a 1.
\(c_i\) são os coeficientes do polinômio definidos pela pelos passos abaixo:
Defina a Matriz de Design \(A\) (Equação 7.8) . A matriz de design \(A\) é formada com base nos termos do polinômio para cada posição na janela. Para um tamanho de janela de \(2u + 1\) e um polinômio de ordem \(m\):
Calcule o produto da matriz \(A^T\) e \(A\).
\[\begin{split}A^T A = \begin{bmatrix} \sum_{i=-u}^{u} i^0 & \sum_{i=-u}^{u} i & \sum_{i=-u}^{u} i^2 & \cdots & \sum_{i=-u}^{u} i^m \\ \sum_{i=-u}^{u} i^1 & \sum_{i=-u}^{u} i^2 & \sum_{i=-u}^{u} i^3 & \cdots & \sum_{i=-u}^{u} i^{m+1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \sum_{i=-u}^{u} i^m & \sum_{i=-u}^{u} i^{m+1} & \cdots & \cdots & \sum_{i=-u}^{u} i^{2m} \end{bmatrix}\end{split}\]Calcule a inversa da matriz \((A^T A)^{-1}\)
Encontre \(A^T A\):
\[(A^T A)^{-1}\]Calcule a Matriz de Coeficientes \(C\)
\[C = (A^T A)^{-1} A^T\]Extraia os Coeficientes \(c_i\)
Os coeficientes \(c_i\) para o filtro são obtidos da primeira linha da matriz \(C\). Normalize os coeficientes, se necessário, para que a soma deles seja igual a 1.
7.2.3. Duplo-logística
Este filtro usa a função logística com dois parâmetros de ajuste para filtrar os dados e foi proposto por Beck et al. [138] para modelar o comportamento temporal do NDVI em áreas de alta latitude (tundra e taiga). Posteriormente, Julien and Sobrino [139], Julien and Sobrino [140] utilizaram este filtro nos dados de NDVI para estimar os parâmetros fenológicos da vegetação de todo o globo terrestre. Para utilizar este filtro é necessário definir 6 parâmetros:
valor mínimo do índice espectral \((w_{IV})\)
valor máximo do índice espectral \((m_{IV})\)
ponto de inflexão da curva quando ela está acendente \((s)\)
ponto de inflexão da curva, um quando ela começa a descendente \((a)\)
a taxa de incremento em \(s (\Delta s)\)
a taxa de decréscimo em \(a (\Delta a)\)
A equação do filtro é apresentada na Equação 7.9:
7.2.4. Séries de Fourier
As séries de Fourier ou Análise harmônica receberam este nome em homenagem a Jean-Baptiste Joseph Fourier, matemático e físico Francês que iniciou a investigação sobre a decomposição de funções periódicas em séries trigonométricas convergentes chamadas séries de Fourier e a sua aplicação aos problemas da condução do calor. Atualmente esta técnica é aplicada nas mais diversas áreas do conhecimento [118, 119].
As séries de Fourier permitem representar uma função complexa por uma somatória de ondas (termos) senoidais e cossenoidais, em que cada onda é definida por um valor único de amplitude e de fase. A amplitude corresponde à metade do valor em que a função é maximizada e a fase (ou ângulo de fase) é o deslocamento entre a origem e o pico da onda no intervalo de \(0\) até \(2 \pi\). Cada termo designa o número de ciclos completados por uma onda num determinado intervalo: o primeiro harmônico ou harmônico fundamental tem um período \(T\) igual ao período total em estudo; o segundo harmônico tem um período igual à metade do período do primeiro harmônico \(\frac{T}{2}\), o terceiro harmônico igual à terceira parte do período \(\frac{T}{3}\) e assim sucessivamente. A somatória dos termos produz uma curva complexa, em que cada componente (termo) representa um percentual do total da variância da série original [118, 119, 141]. A representação gráfica desse processo pode ser observada na Figura 7.4.
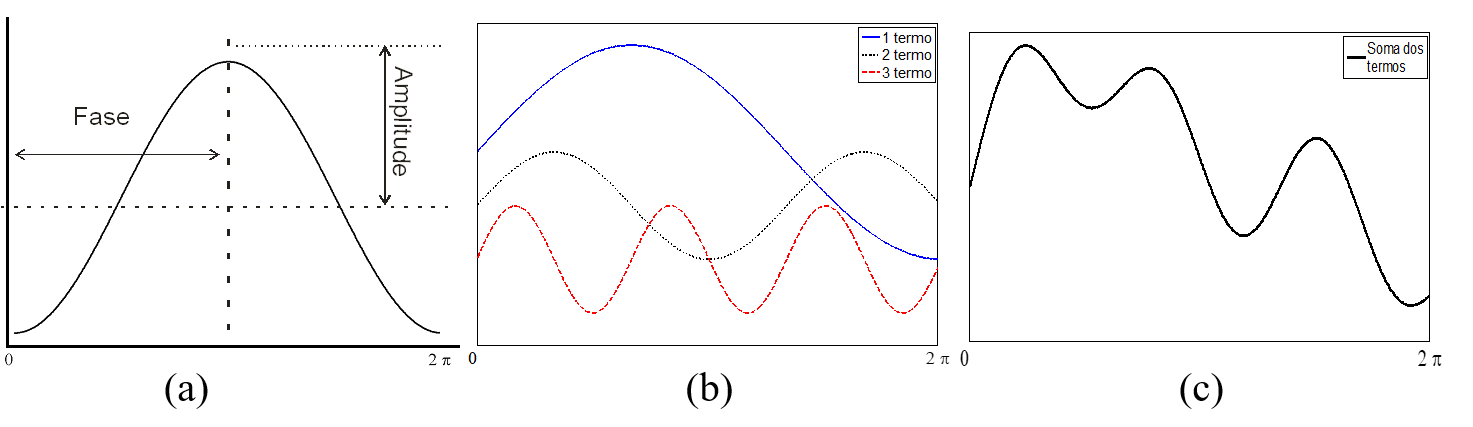
Figura 7.4 - Séries de Fourier e harmônicos. (a) Curva de cosseno representando o primeiro harmônico; (b) curvas para os primeiros três harmônicos; (c) curva resultante da somatória dos três harmônicos.
Uma série temporal de \(N\) amostras eqüidistantes, de uma variável \(y\), pode ser representada por uma função harmônica. Esta função pode ser utilizada então para a estimativa de valores ao longo do tempo (\(t\)), permitindo a reconstrução da curva [118, 119, 141]. Neste caso, um valor da variável \(y\), em uma data \(i\) pode ser estimado por meio da Equação 7.10:
em que: \(\overline{y}\) representa a média dos valores da série de dados, \(C_j\) representa a amplitude, \(\omega_j\) representa a frequência, \(\phi_j\) o ângulo de fase.
É possível escrever a equação anterior utilizando a função seno. No entanto, a função cosseno é geralmente utilizada, pois o ângulo de fase pode ser facilmente determinado como correspondendo ao tempo (t) no qual a função harmônica é maximizada (Equação 7.11)
A amplitude (\(C_j\)) é estimada por meio da Equação 7.12
em que \(A_j\) obtido pela Equação 7.13 e \(B_j\) obtido pela Equação 7.13 são as componentes de cosseno e seno do vetor amplitude, respectivamente:
O ângulo de fase (\(\phi_j\)) é definido por meio da Equação 7.15: