10.2. Métodos de Agrupamento de Séries Temporais
Na literatura, existem diferentes métodos para agrupamento de dados. Segundo [184], esses métodos podem ser classificados em: (1) Métodos baseados em partição que criam partições ortogonais em um conjunto de dados (ex.: K-means); (2) Métodos baseados em hierarquia que criam uma decomposição hierárquica em conjunto de dados (ex.: Hierarchical Clustering); (3) Métodos que criam grupos com base em densidade (ex.: DBSCAN); e (4) Métodos baseados em Redes Neurais (ex. SOM).
Para agrupamento de séries temporais, um dos métodos mais utilizado é o SOM (Self-Organizing Maps), ou Mapas Auto-organizáveis em português, que é uma rede neural artificial [177]. As redes neurais artificiais (do inglês, Artificial Neural Networks, ANNs) são métodos inspirados em redes neurais biológicas e possui aplicações tanto em tarefas de classificação como em agrupamento [185]. Algumas características das ANNs que são importantes nos métodos de agrupamento são: processamento de vetores numéricos; arquiteturas de processamento inerentemente paralelas e distribuídas e aprendizado a partir de pesos por interconexões.
Muitas metodologias de agrupamento de séries temporais de imagens utilizam o SOM combinado com um HCA (Hierarchical Clustering Algorithm) ou Algoritmo de Agrupamento Hieráquico em português [186].
10.2.1. SOM (Self-Organizing Maps)
O SOM (Self-Organizing Map) é uma rede neural não supervisionada, que aplica o procedimento de aprendizado competitivo para mapear os vetores de entrada multidimensionais para uma grade bidimensional retangular ou hexagonal de baixa dimensão [187]. SOM mapeia um espaço de alta dimensão para um espaço de baixa dimensão preservando sua topologia de vizinhança. Ele é composto por uma camada de entrada (input layer) e uma de saída (output layer), sendo esta última geralmente uma grade bidimensional onde cada elemento é chamado de neurônio (2-D Neuron Grid). Uma propriedade importante do SOM é que os neurônios são organizados de forma que eles mantenham uma vizinhança similar, ou seja, neurônios que têm características similares estão próximos na camada de saída. Figura 10.9 e Figura 10.10 ilustram as camadas do SOM e a similaridade entre neurônios vizinhos.
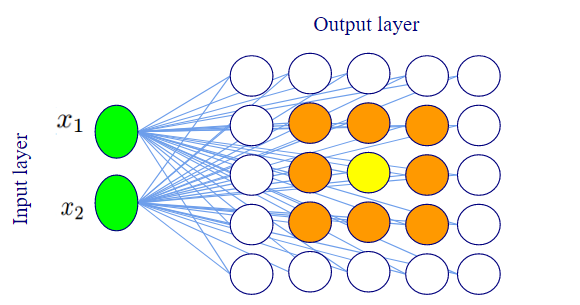
Figura 10.9 - Camadas de entrada (input layer) e saída (output layer) do SOM (Self-Organizing Map). No mapa ou camada de saída, os neurônios pintados em laranja são vizinhos do neurônio amarelo.
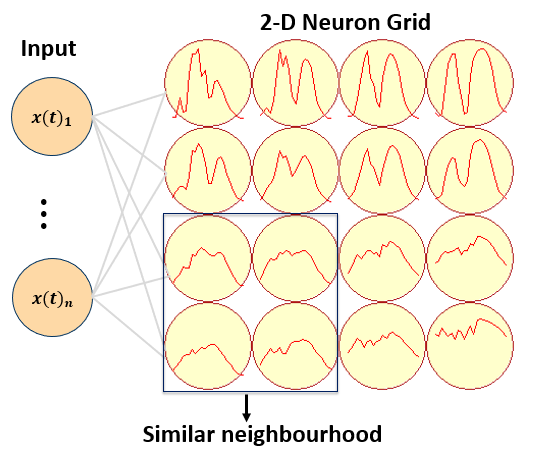
Figura 10.10 - Um exemplo de uma mapa SOM 4x4. O vetor de entrada (input) é mapeado para uma grade de saída composta por neuônios (2-D Neuron Grid). O neurônio mais similar ao vetor de entrada adapta seu vetor de peso (weight vector) e dos seus neurônios vizinhos, gerando uma vizinhança similar.
Fonte: [188].
Cada neurônio \(j\) tem um vetor de peso (weight vector) n-dimensional \(w_j=[w_{1},\ldots,w_{n} ]\). Um vetor de entrada \(x(t)=[x(t)_1,\ldots,x(t)_n ]\) é associado ao neurônio mais similiar a ele, segundo uma certa métrica de distância, como Euclidiana e DTW. A distância \(D_j\) é computada entre o vetor de entrada e o vetor de peso de cada neurônio \(j\), para todos os neurônios da camada de saída:
Depois de computar todas as distâncias entre o vetor de entrada e todos os neurônios, a menor dessas distâncias identifica o Best-Matching-Unit (BMU). O BMU é o neurônio \(d_{b}\) cujo vetor de peso é o mais próximo, ou mais similar, a \(x(t)\):
Os vetores de peso do BMU e de seus vizinhos dentro de um raio \(r\) são alterados para aumentar a similaridade com o vetor de entrada:
onde \(\alpha(t)\) representa a taxa de aprendizado (learning rate), com valores entre 0 e 1 (\(0<\alpha(t)<1\)), e \(h_{b,j}\) é uma função de vizinhança (neighborhood function).
O SOM termina quando todos os vetores de entrada são representados na camada de saída. Ao longo do tempo, o valor de \(\alpha(t)\) e o raio da vizinhança devem ser reduzidos e existem diferenteres abordagens para reduzir esses valores [189].
Em resumo, no mapa SOM os neurônios competem entre si pelos vetores de entrada. Ao final de cada iteração é determinado o neurônio vencedor (BMU, do inglês Best Match Unit), aquele que possui a menor distância com o vetor de entrada apresentado na iteração. Após a escolha do BMU, todos os neurônios vizinhos em um determinado raio atualizam seus vetores de peso, para se aproximarem do padrão escolhido no BMU [187]. A Figura 10.11 a seguir apresenta uma visão geral da estrutura do SOM.
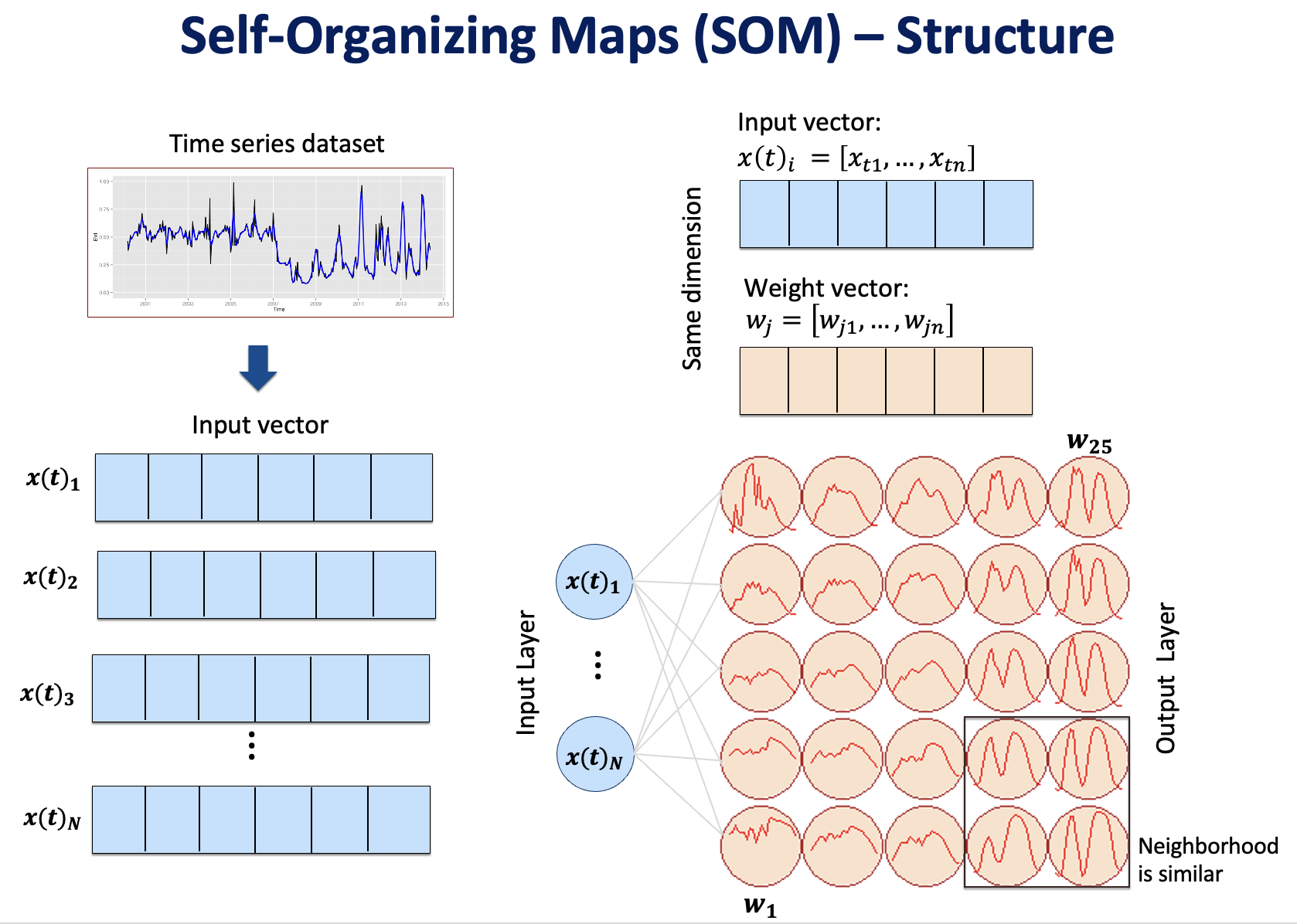
Figura 10.11 - Estrutura geral do SOM (Self-Organizing Map).
Adaptado de: [190]
10.2.2. Evolving SOM (Self-Organizing Maps)
No SOM, o tamanho da grade ou da camada de saída é fixo e definido a priori. Muitos trabalhos na literatura apontam que a definição do tamanho dessa grade é um processo empírico. A quantidade de vetores de entrada influencia no tamanho da grade [187]. Grade superestimada implica em neurônios vazios sem nenhum vetor de entrada associado, ou neurônios sem capacidades de generalização, com um único vetor de entrada associado. Subestimar a grade implica em neurônios generalistas e erros de agrupamento.
Para tentar resolver essa questão do tamanho da grade fixa do SOM, algumas variações do SOM são propostas para evoluir a grade dinamicamente ao invés de definir seu tamanho inicialmente. Essas abordagens são chamadas de Evolving SOM e alguns exemplos são: (1) Growing hierarchical self-organizing maps (GHSOM) [191]; (2) Growing cell structure of map (GCS) [192]; e (3) Growing SOM (GSOM) [193].
A Figura 10.12 mostra mapas gerados pelo SOM e pelo GSOM para séries temporais de imagens, resultado do trabalho de Adeu et. al [188].
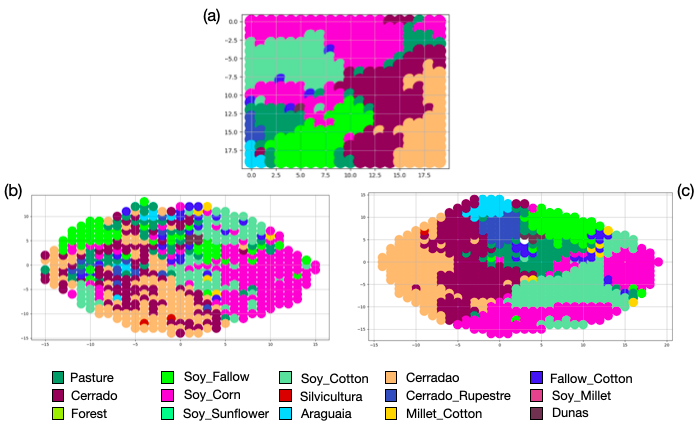
Figura 10.12 - A topologia do mapa do SOM (a), do GSOM com initial neighborhood influence 0.6 (b) e com initial neighborhood influence 1.0 (c). O aumento do parâmetro do GSOM initial neighborhood influence resulta em clusters mais concisos e agrupados.
Adaptado de: [188]
10.2.3. HCA (Hierarchical Clustering Algorithm)
O Hierarchical Clustering Algorithm (HCA) é um método que particiona os dados sucessivamente, criando uma hierarquia de agrupamentos [186]. Existem dois tipos de agrupamento hierárquico: aglomerativo e divisivo.
No HCA divisivo, todo o conjunto de dados começa em um único agrupamento e a cada iteração os grupos vão se dividindo em agrupamentos semelhantes. No HCA aglomerativo cada dados de entrada é um agrupamento e a cada iteração os grupos vão se juntando em agrupamentos semelhantes. Em cada etapa, os agrupamentos são mesclados e a hierarquia é construída com base em critérios de ligação (linkage criteria em inglês).
O critério de ligação indica como as medidas de distância (ou a similaridade) entre os agrupamentos são calculadas. Existem vários critérios de ligação propostos na literatura. Os métodos mais comuns são ligação simples, completa e média. No critério de ligação simples, a proximidade entre dois clusters é calculada pela menor distância entre eles, enquanto na ligação completa é calculada pela distância máxima entre eles. Na ligação média, a distância média é calculada entre todos os elementos de dois clusters [186]. Além desses critérios, existem outros como a ligação por centroide e a ligação de Ward. Na ligação por centroide, o centro dos elementos dos clusters é usado para calcular a distância entre eles, e a ligação de Ward usa a variância mínima para encontrar a similaridade entre os clusters.
O HCA constrói uma árvore binária chamada dendrograma. Essa estrutura representa a ordem em que os agrupamentos foram mesclados. Um dendrograma divide os dados em grupos internamente homogêneos entre si. A variabilidade dos dados pode ser visualizada usando a hierarquia da árvore. O objetivo do dendrograma é explorar e definir o número adequado de clusters com base na variação de similaridade entre eles. Figura 10.13 e Figura 10.14 ilustram um dendrogram e a seleção de 4 e 3 clusters, baseado na similaridade entre eles.
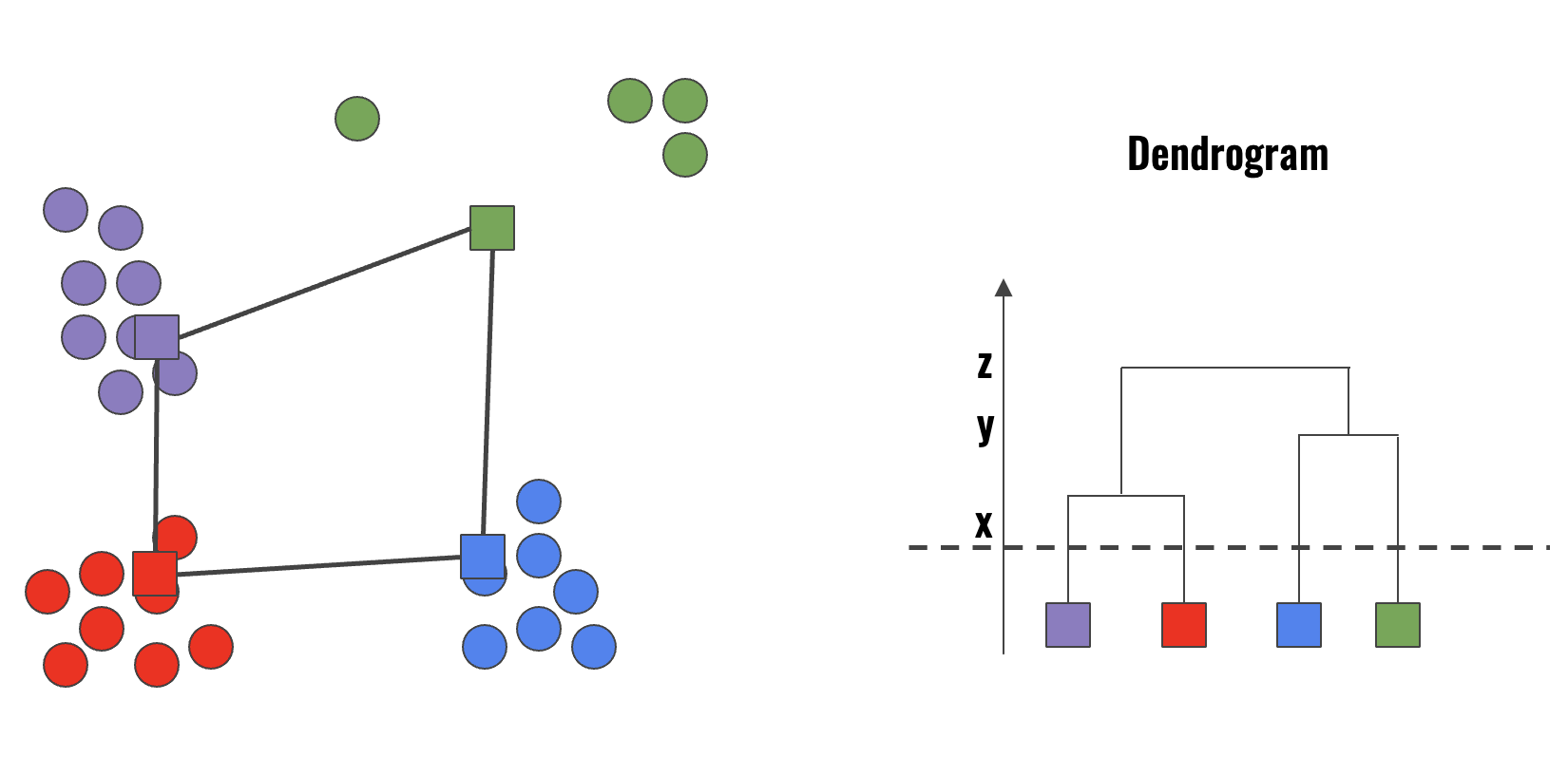
Figura 10.13 - Ilustração de um dendrogram e a seleção de 4 clusters.
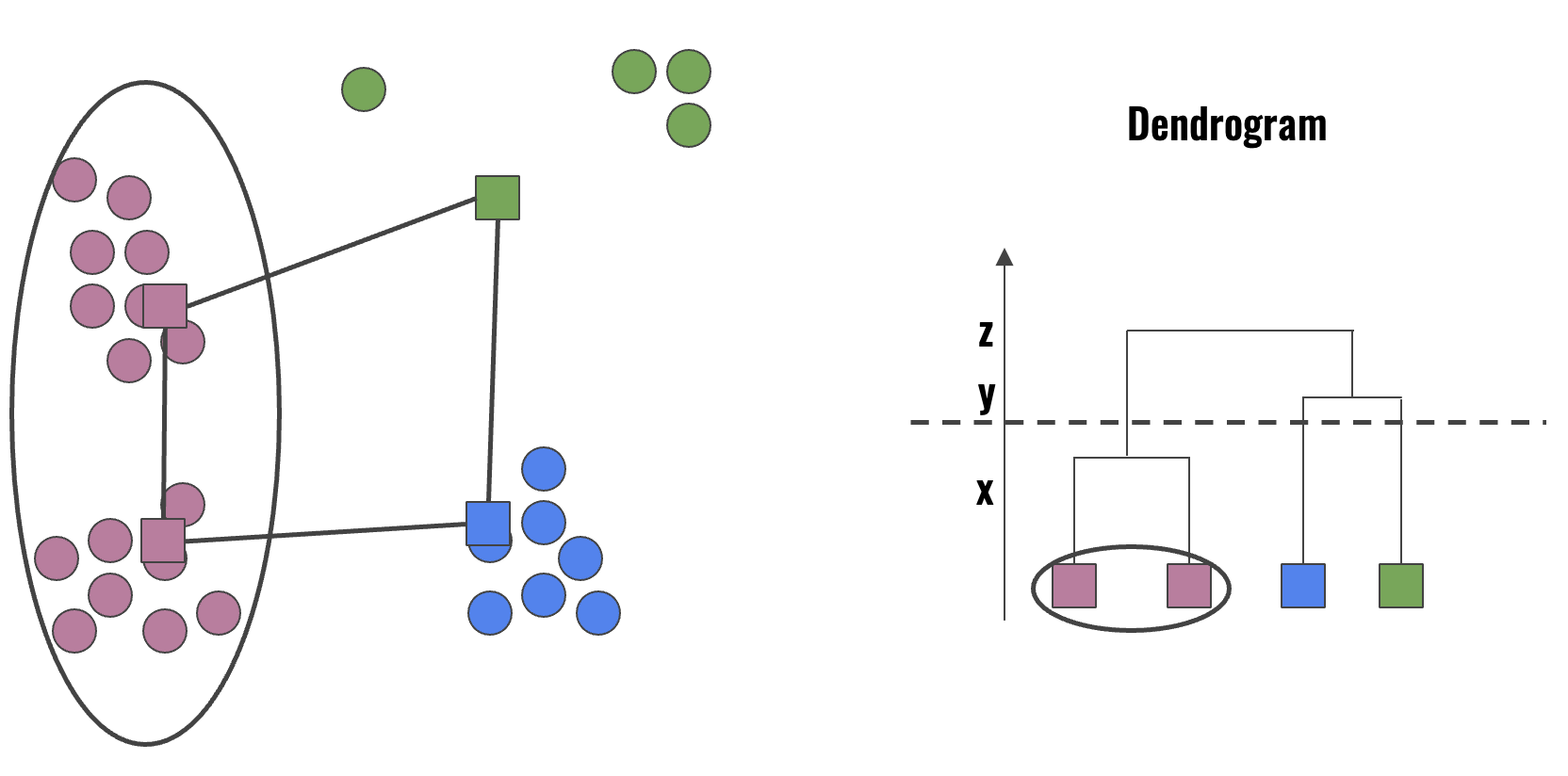
Figura 10.14 - Ilustração de um dendrogram e a seleção de 3 clusters.