10.1. Medidas de Similaridade entre Séries Temporais
Existem diferentes medidas de similaridade para séries temporais [177], como mostrado na Figura 10.4. Essas medidas incluem Hausdorff, Modified Hausdorff (MODH), HMM-based distance, Dynamic Time Warping (DTW), Euclidean distance, Euclidean distance in a PCA subspace, and Longest Common Sub-Sequence (LCSS).
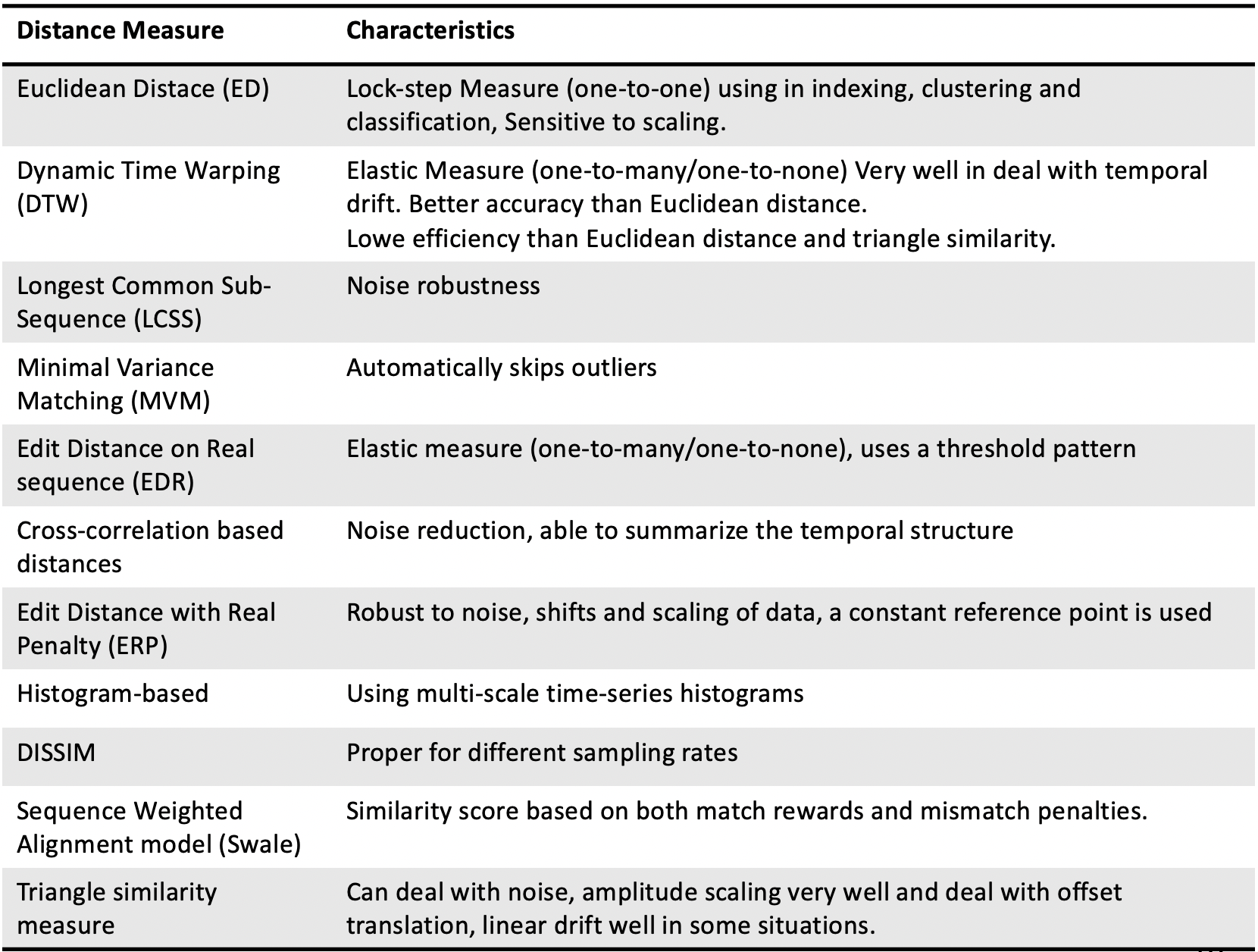
Figura 10.4 - Medidas de similaridades entre séries temporais baseadas na forma.
Adaptado de: [177].
A escolha de uma abordagem de distância adequada depende das características das séries temporais, da duração das séries, do método de representação e do objetivo do agrupamento (similaridade no tempo, na forma ou na mudança). As distâncias mais utilizadas para similaridade entre séries temporais são: Euclidiana e DTW (e suas variações). Figura 10.5 e Figura 10.6 ilustram a diferença entre as distâncias DTW e Euclidiana entre duas séries temporais.
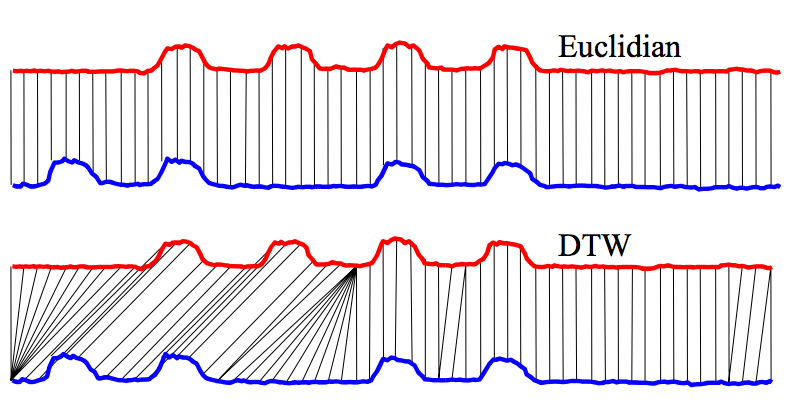
Figura 10.5 - Distâncias DTW e Euclidiana entre duas séries temporais.
Fonte: [181].
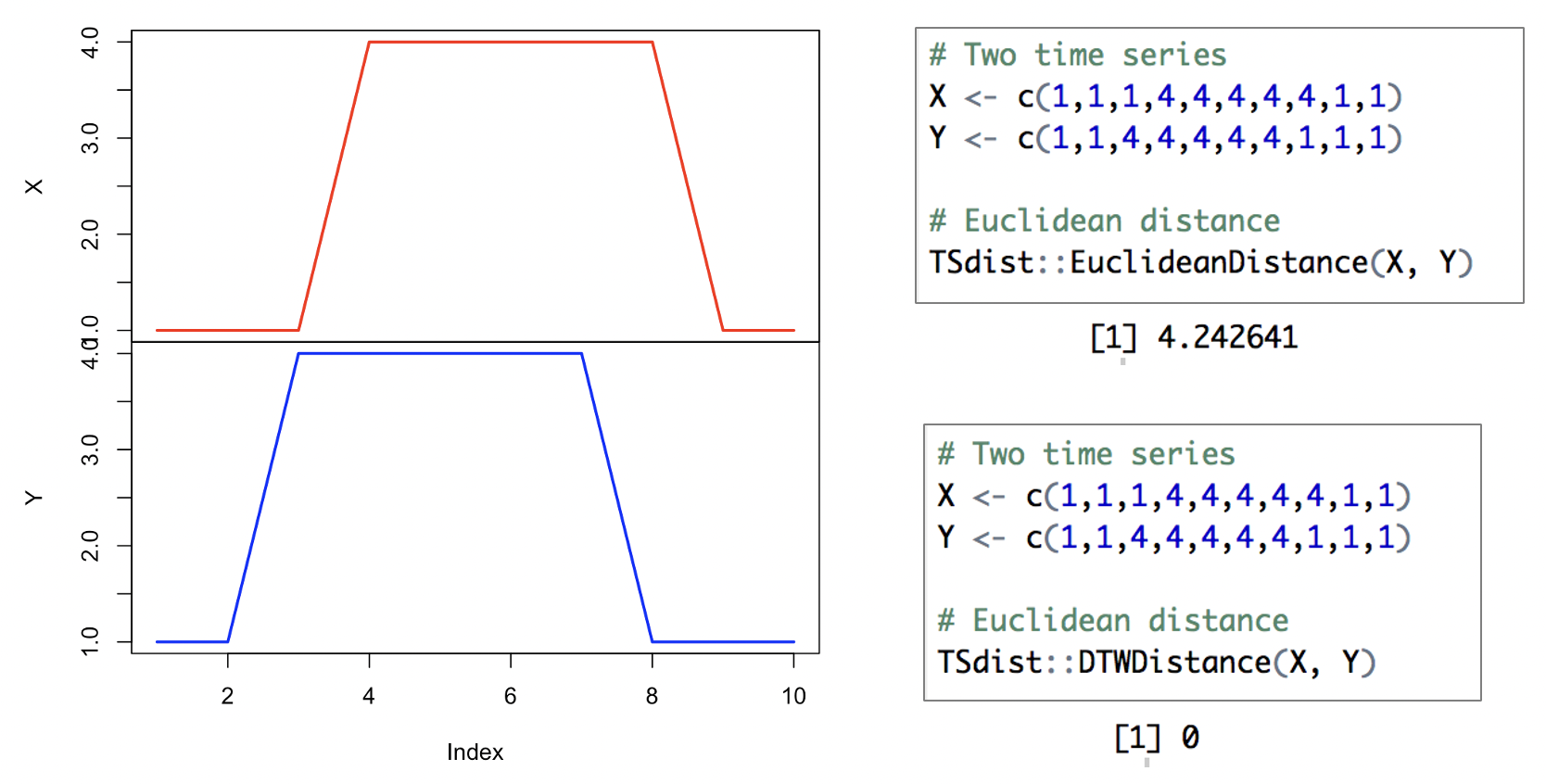
Figura 10.6 - Distâncias DTW e Euclidiana entre duas séries temporais calculadas no ambinete R utilizadno o pacote TSDist.
10.1.1. Distância Euclidiana
A distância euclidiana e suas variações, como Manhattan, são amplamente utilizadas em métodos de agrupamento devido suas simplicidades e eficiência linear \(O(n)\). Baseada em comparações ponto a ponto (lock-step), em que assume que o i-ésimo ponto de uma série esteja alinhado com o i-ésimo ponto na outra série, como ilustrado nas figuras anteriores, a distância euclidiana é limitada a séries temporais com a mesma linha de base, escala e comprimento. Além disso, ela ignora os desalinhamentos nos eixos temporais.
Definição: Dado duas séries temporais \(i = (x_{i1}, x_{i2},...,x_{in})\) e \(j = (x_{j1}, x_{j2},...,x_{jn})\) com n valores.
A distância euclidiana entre essas duas séries é definida como:
A distância manhattan entre essas duas séries é definida como:
10.1.2. Distância DTW (Dynamic Time Warping)
Dado duas séries temporais, a distância DTW (Dynamic Time Warping) as esticam ou comprimem localmente para fazer com que uma se pareça com a outra o máximo possível [183]. Por isso a distância DTW é chamada de elástica. Ela contorna o problema de desalinhamento temporal, pois permite uma mudança elástica no eixo do tempo, como ilustrado na Figura 10.7. A distância entre as duas séries é computada após o alongamento, somando as distâncias entre os elementos alinhados. Essa distância baseia-se em técnicas de programação dinâmica, sendo mais robusta que a distância euclidiana, no entanto, sem otimizações possui complexidade de \(O(n^2)\) [181].
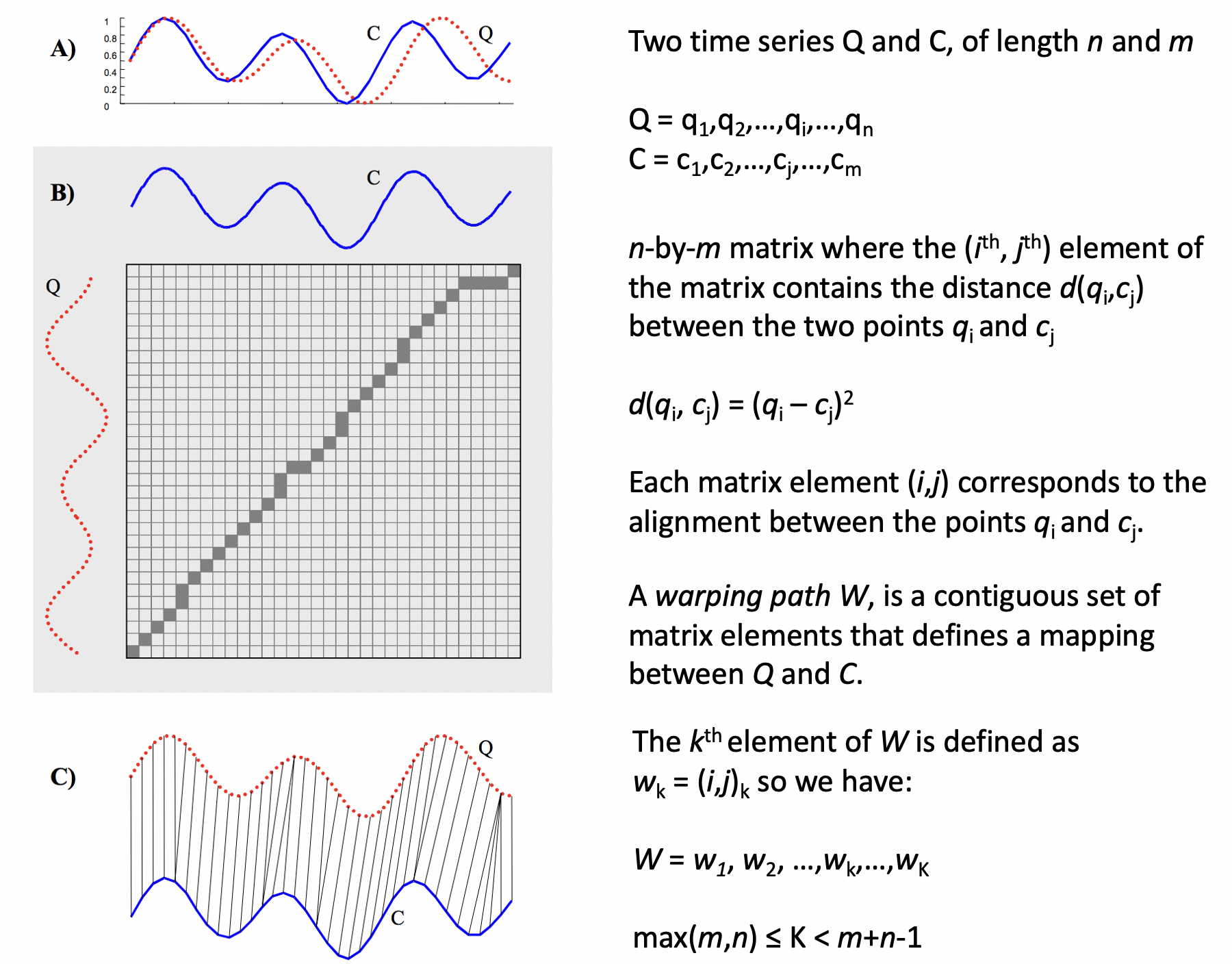
Figura 10.7 - Distância DTW (Dynamic Time Warping) entre duas séries temporais.
Adaptada de: [181].
Definição: Dado duas séries temporais \(Q = q_1, q_2,..., q_n\) e \(C = c_1, c_2,...,c_m\). Para alinhar ambas sequências, uma matriz \(n\) x \(m\) é construída, em que cada elemento \((i_{th}, j_{th})\) contém a distância entre \(q_i\) e \(c_j\), como por exemplo \(d(q_i, c_j) = (q_i - c_j)^2\). Cada elemento \((i,j)\) da matriz corresponde ao alinhamento entre os pontos \(q_i\) e \(c_j\). Uma via de deformação (ou Warping Path) \(W\) é um traçado de elementos contíguos na matriz, que define um mapeamento entre \(Q\) e \(C\). O elemento \(k^{th}\) de \(W\) é definido como \(w_k = (i,j)_k\). Assim, \(W = w_1, w_2,...,w_k\) é obtido com \(\max(m,n) \leq K < m + n - 1\). Geralmente, o caminho na matriz é diagonal, começando em extremos opostos da matriz, por exemplo \(w_1 = (1, 1)\) e \(w_k = (m,n)\). Desta forma, o objetivo é selecionar o caminho que minimize o custo da via de deformação:
Para restringir o quanto a via de deformação (ou Warping Path) pode desviar da diagonal da matriz, é possível definir a janela de deformação (ou Warping Window). A Figura 10.8 ilustra dois tipos de janelas mais usadas como restrição global no DTW: Sakoe-Chiba Band and the Itakura Parallelogram.
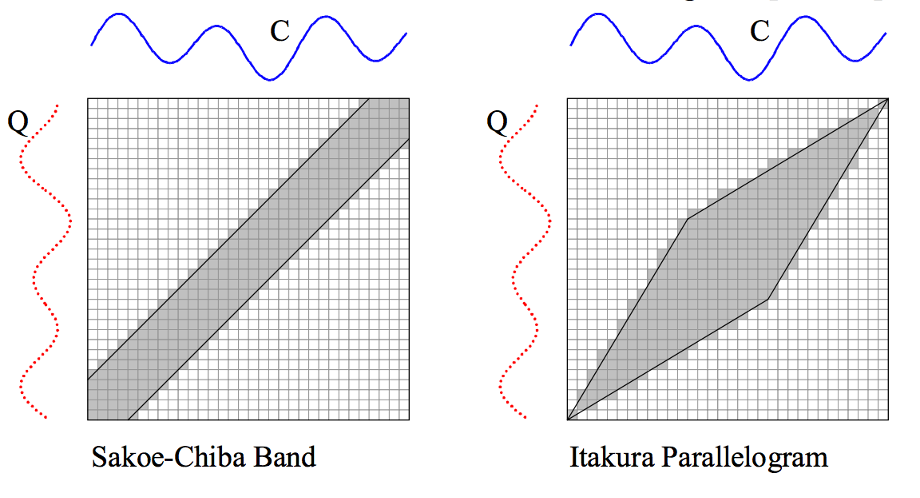
Figura 10.8 - Janela de deformação (ou Warping Window) do DTW (Dynamic Time Warping).
Fonte: [181].