6.4. Composição colorida e Contraste
Para construir uma composição colorida a partir de um conjunto de imagens, precisamos informar quais bandas serão utilizadas nas componentes RGB do gráfico:
canal R (Red, vermelho)
canal G (Green, verde)
canal B (Blue, azul)
Para isso, podemos criar uma matriz NumPy com 3 dimensões, as quais estão relacionadas às quantidades de linhas, colunas, e bandas, e a biblioteca Matplotlib produzirá uma visualização colorida.
O contraste é uma técnica que melhora a visualização da imagem. Veja que neste caso, os números digitais da imagem podem ser alterados, e assim as propriedades dos elementos em relação a suas respostas espectrais ficam comprometidas.
Nota
Para realizar análises baseadas no comportamento espectral de alvos, técnicas de contraste devem ser evitadas. Por exemplo, o índice espectral NDVI não pode ser computado utilizando canais alterados por contraste.
Uma maneira bem conhecida de aplicar o contraste é através das operações de gain (usualmente chamada ganho) e offset. O gain é um valor constante que é multiplicado por todos os pixels das imagens. O offset, que representa um deslocamento, é um valor constante que é somado a todos os pixels das imagens. Para aplicar este tipo de contraste, bem como outros que veremos a seguir, é importante ter conhecimento da propriedade quantização das imagens (Seção 6.1.6), e também sobre como as bibliotecas de visualização trabalham com os intervalos de representação. A quantização, representada por \(L\), indica a quantidade de bits utilizados para armazenar cada pixel. Por exemplo, o satélite AMAZONIA-1 possui \(L = 10\). Nesse caso, os pixels das imagens do AMAZONIA-1 possuem valores variando entre 0 e \(2^{10} = 1024\). No entanto, muitas vezes a distribuição de valores dos pixels não está espalhada em todo esse intervalo. Dessa forma, a visualização da imagem acaba ficando opaca. Assim, técnicas de contraste visam transformar o intervalo de pixels, muitas vezes mal distribuído, de forma a utilizar todo o intervalo de representação.
Para melhor visualizar a imagem, espera-se que a distribuição dos pixels maximize o intervalo de representação. Uma forma de fazer isso é por meio de técnicas de normalização. Uma forma eficiente de normalizar uma imagem consiste em aplicar uma função que transforme o menor valor de pixel encontrado em \(0\), e o maior valor de pixel encontrado em \(L - 1\), usando a fórmula apresentada na Equação 6.1:
onde: \(P\) se refere ao valor atual do pixel, \(Q\) é o valor resultante da transformação, e \(\min_{pixel}, \max_{pixel}\) são, respectivamente, os valores do maior e do menor valor de pixel encontrados na imagem original.
É possível também realizar outras transformações nas imagens, como por exemplo aplicar uma função matemática sobre todos os pixels, e assim a forma da função vai gerar uma alteração na relação entre os valores originais. Se aplicarmos a função raiz quadrada sobre cada pixel, conforme a Equação 6.2, veremos que essa função tem uma angulação acentuada nos menores valores, e a angulação vai reduzindo conforme os valores aumentam. Isso acaba produzindo um efeito de gerar alto contraste nas áreas escuras da imagem, e um contraste reduzido nas áreas mais claras da imagem.
onde: \(P\) se refere ao valor atual do pixel, \(Q\) é o valor resultante da transformação.
De forma oposta, ao aplicar a função quadrado nos pixels da imagem, conforme a Equação 6.3, nota-se que a curva tem ângulo reduzida na região das áreas escuras da imagem, e um contraste acentuado nas áreas mais claras da imagem.
onde: \(P\) se refere ao valor atual do pixel, \(Q\) é o valor resultante da transformação.
Nota
Algumas transformações podem gerar valores fora do intervalo de representação. Assim, é comum aplicar uma determinada função, como raiz ou quadrado, por exemplo, e depois ter que aplicar uma normalização dos valores para que voltem a ficar no intervalo de representação. Quando essa operação não é realizada, pode ser observado um efeito de saturação dos pixels com valores extremos, tanto os mais claros quanto os mais escuros. Dependendo do sistema de visualização, os resultados podem parecer incoerentes.
A Figura 6.14 apresenta uma composição colorida original (sem contraste), e a aplicação do contraste por ganho e offset, além da normalização das bandas e a aplicação de duas funções de contraste, o quadrado e a raiz.
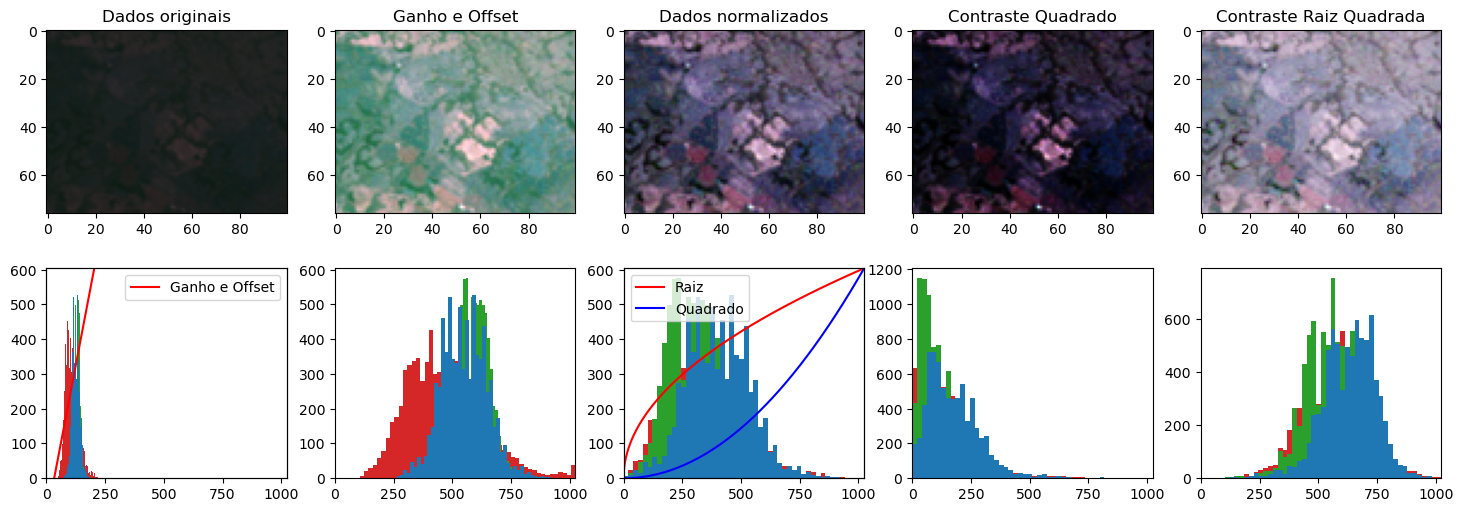
Figura 6.14 - Visualização da composição colorida original e o resultado da aplicação de diferentes contrastes.